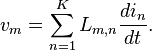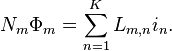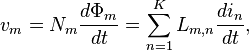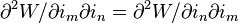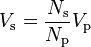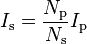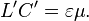This is a Heading

This is a paragraph.

Induktansi

Induktansi adalah sifat dari rangkaian elektronika yang menyebabkan timbulnya potensial listrik secara proporsional terhadap arus yang mengalir pada rangkaian tersebut, sifat ini disebut sebagai induktansi sendiri. Sedang apabila potensial listrik dalam suatu rangkaian ditimbulkan oleh perubahan arus dari rangkaian lain disebut sebagai induktansi bersama.

Definisi kuantitatif dari induktansi sendiri (simbol: L) adalah


dimana v adalah GGL yang ditimbulkan dalam volt dan i adalah arus listrik dalam ampere. Bentuk paling sederhana dari rumus tersebut terjadi ketika arus konstan sehingga tidak ada GGL yang dihasilkan atau ketika arus berubah secara konstan (linier) sehingga GGL yang dihasilkan konstan (tidak berubah-ubah).

Istilah 'induktansi' sendiri pertama kali digunakan oleh Oliver Heavside pada Februari 1886. Sedang penggunaan simbol L kemungkinan ditujukan sebagai penghormatan kepada Heinrich Lenz, seorang fisikawan ternama. Satuan induktansi dalam Satuan Internasional adalah weber per ampere atau dikenal pula sebagai henry (H), untuk menghormati Joseph Henry seorang peneliti yang berkontribusi besar terhadap ilmu tentang magnetisme. 1 H = 1 Wb/A.

Induktansi muncul karena adanya medan magnet yang ditimbulkan oleh arus listrik (dijelaskan oleh Hukum Ampere). Supaya suatu rangkaian elektronika mempunyai nilai induktansi, sebuah komponen bernama induktor digunakan di dalam rangkaian tersebut, induktor umumnya berupa kumparan kabel/tembaga untuk memusatkan medan magnet dan memanfaatkan GGL yang dihasilkannya.

Bentuk umum dari K buah rangkaian dengan arus i_m dan tegangan v_m adalah


Koefisien L yang digunakan pada rumus di atas merupakan matriks simetris, rumus tersebut berlaku selama tidak menggunakan bahan yang bisa menjadi magnet, jika tidak maka besaran L merupakan fungsi dari besaran arus (induktansi non-linier).

Penerapan Persamaan Maxwell untuk induktansi

Rumus umum di atas merupakan penerapan dari Persamaan Maxwell jika rangkaian tersebut menggunakan kabel tipis.

Misal suatu rangkaian yang terdiri dari K buah kumparan kabel, masing-masing terdiri dari satu atau beberapa lilitan. Fluks magnetik yang timbul akan terangkai sebesar


Dimana Nm merupakan jumlah lilitan dalam kumparan m, Φm adalah fluks magnetik yang melalui kumparan, dan Lm,n adalah konstanta. Persamaan ini diturunkan dari Hukum Ampere--medan magnet dan fluks magnetik merupakan fungsi linier dari arus listrik. Dengan menggunakan Hukum Faraday dapat diperoleh


dimana vm merupakan GGL yang terinduksi dalam rangkaian m. Rumus tersebut sesuai dengan definisi di atas bahwa koefisien Lm,n dapat diidentifikasi sebagai koefisien induktansi. Karena seluruh arus Nnin berperan menimbulkan fluks Φm, dapat pula dimengerti bahwa Lm,n sebanding dengan perkalian jumlah lilitan NmNn.

Induktansi dan Energi Medan Magnet

Dengan mengalikan persamaan vm di atas dengan imdt dan menjumlahkan untuk semua m maka kita dapatkan energi yang di transfer sistem ini dalam satu satuan waktu dt,


Hal ini harus tetap sesuai dengan perubahan energi medan magnet W yang ditimbulkan oleh arus listrik. Integritas


mengharuskan Lm,n=Ln,m. Sehingga Lm,n harus merupakan matriks simetris.

Integral dari energi yang ditransfer adalah energi medan magnet sebagai fungsi dari arus,


Persamaan ini juga merupakan konsekuensi dari linearitas Persamaan Maxwell. Supaya mudah mengingat perlu diperhatikan bahwa perubahan arus listrik berhubungan langsung dengan perubahan energi medan magnet. Energi ini memerlukan sumber tegangan (jika negatif, energi diambil) atau menghasilkan tegangan (jika energi positif, disalurkan). Analoginya dalam energi mekanis untuk K = 1 dengan energi medan magnetik (1/2)Li2 adalah sebuah benda dengan masa M, dengan laju u dan energi kinetiknya (1/2)Mu2. Energi dari perubahan laju (dalam hal elektronika, arus listrik) dikalikan masa benda (induktansi) diperoleh dari gaya (jika energi kinetik bertambah) atau menghasilkan gaya (jika energi kinetik berkurang).

Induktor yang Berpasangan (Kopling Induktor)

Diagram rangkaian yang menggambarkan dua buah induktor di pasangkan.
Dua garis vertikal di antara induktor menunjukkan inti padat yang mana pada inti ini kawat lilitan induktor dililitkan. "n:m" menunjukkan perbandingan jumlah lilitan antara induktor sebelah kiri dengan yang sebelah kanan. Gambar ini juga menunjukkan konvensi titik.

Induktansi bersama muncul ketika perubahan arus dalam satu induktor menginduksi (mempengaruhi) timbulnya GGL di induktor lain yang ada di dekatnya. Mekanisme ini merupakan dasar yang sangat penting dalam cara kerja transformer, namun kadang kala induksi bersama yang bisa terjadi antara konduktor yang berdekatan malah menjadi hal yang harus dihindari dalam suatu rangkaian.

Induktansi bersama, M, juga merupakan ukuran saling induksi antara dua buah induktor. Induktansi bersama oleh rangkaian i kepada rangkaian j dihitung menggunakan integral ganda Rumus Neumann.

Induktansi bersama memiliki hubungan persamaan:


dimana
adalah nilai induktansi bersama, dan tanda 21 menunjukkan keterkaitan GGL yang terinduksi dalam kumparan 2 disebabkan oleh perubahan arus dalam kumparan 1.
N1 adalah jumlah lilitan pada kumparan 1,
N2 adalah jumlah lilitan pada kumparan 2,
P21 adalah permeansi ruang dimana fluks magnetik berada.
Induktansi bersama juga memiliki keterkaitan dengan koefisien kopling. Koefisien kopling bernilai antara 1 dan 0, koefisien kopling digunakan sebagai indikator keterkaitan antara induktor yang dipasangkan (dikopling).


dimana

k adalah koefisien kopling dan 0 ≤ k ≤ 1,
L1 adalah nilai induktansi kumparan pertama, dan
L2 adalah nilai induktansi kumparan kedua.
Jika nilai induktansi bersama, M, sudah diketahui, maka nilai ini dapat digunakan untuk memprediksi sifat dari suatu rangkaian:


dimana

V1 adalah tegangan dalam induktor yang dihitung,
L1 adalah induktansi dalam induktor yang dihitung,
dI1/dt adalah arus (diturunkan atas waktu) yang mengalir dalam induktor yang dihitung,
dI2/dt adalah arus (diturunkan atas waktu) yang mengalir dalam induktor yang dikopling (diinduksi oleh induktor pertama), dan
M adalah nilai induktansi bersama.
Tanda minus muncul karena menurut konvensi titik, kedua arus yang mengalir pada masing-masing induktor saling berlawanan arah.

Jika suatu induktor dipasangkan secara berdekatan dengan induktor lain dengan menggunakan prinsip induktansi bersama, seperti dalam transformer, maka tegangan, arus, dan jumlah lilitan dapat dihubungkan sebagai berikut:


dimana

Vs adalah tegangan pada induktor sekunder,
Vp adalah tegangan pada induktor primer (yaitu yang terhubung dengan sumber listrik),
Ns adalah jumlah lilitan pada induktor sekunder, dan
Np adalah jumlah lilitan pada induktor primer.
Begitu pula untuk arus:


dimana

Is adalah arus yang mengalir dalam induktor sekunder,
Ip adalah arus yang mengalir dalam induktor sekunder (yaitu yang terhubung dengan sumber listrik),
Ns adalah jumlah lilitan pada induktor sekunder, dan
Np adalah jumlah lilitan pada induktor primer.
Perlu diperhatikan bahwa daya dari kedua induktor tersebut adalah sama. Juga persamaan di atas tidak berlaku jika kedua induktor memiliki sumber energi sendiri-sendiri (keduanya induktor primer).

Jika kedua sisi transformer merupakan rangkaian LC yang mana frekuensi tegangan menjadi penting, nilai induktansi bersama antara dua lilitan ini menentukan bentuk dari kurva renspon frekuensi. Walaupun batas-batas nilai indutansi bersama ini tidak didefinisikan, namun sering disebut sebagai loose-coupling, critical-coupling, dan over-coupling. Jika rangkaian tersebut melalui transformer yang loose-coupling, bandwidth-nya akan sempit. Ketika nilai induktansi bersama ditingkatkan, bandwidth-nya ikut naik pula. Ketika nilai induktansi bersama telah melampaui titik kritis, respon bandwidth akan mulai menurun, frekuensi-frekuensi tengah akan teratuentasi lebih dibanding frekuensi-frekuensi samping. Kondisi ini disebut over-coupling.

Rumus Perhitungan

Umumnya, induktansi dapat dihitung menggunakan persamaan Maxwell. Pada banyak skenario perhitungan dapat disederhanakan dari persamaan Maxwell. Jika menginginkan induksi dengan arus berfrekuensi tinggi, dengan efek kulit, arus listrik dan medan magnet pada permukaan konduktor dapat dihitung dengan menggunakan persamaan Laplace. Walaupun konduktor yang digunakan adalah kawat tipis, induktansi sendiri masih bergantung pada jari-jari penampang kawat dan distribusi arus dalam kawat tersebut. Distribusi arus ini rata-rata konstan (pada permukaan atau badan kawat) untuk kawat tipis.

Induktansi bersama

Induktansi bersama dalam rangkaian kumparan i kepada rangkaian j dinyatakan dalam integral ganda Rumus Neumann


Simbol μ0 menunjukkankonstanta magnetik (4π×10−7 H/m), 'Ci dan Cj adalah panjang kawat, Rij adalah jarak antara dua induktor.

Induktansi sendiri

Pada dasarnya induktansi sendiri dari kumparan kawat dapat dinyatakan pula dengan persamaan di atas dengan menganggap i=j. Masalahnya, 1/R menjadi tidak terdefinisi, sehingga perlu menyatakan penampang a sebagai penampang kawat dan memperhatikan pula distribusi arus pada kawat tersebut. Sehingga ada integral untuk semua titik dimana |R| ≥ a/2,


Disini a dan l menunjukkan jari-jari penampang kawat dan panjang kawat, dan Y adalah konstanta yang tergantung pada distribusi arus dalam kawat: Y = 0 ketika arus mengalir pada permukaan kawat (efek kulit), Y = 1/2 ketika arus tersebar rata dalam kawat. Nilai-nilai ini hanya perkiraan namun cukup akurat jika kawat yang dipergunakan tipis dan panjang.

Hubungan induktansi dan kapasitansi

Induktansi per satuan panjang L' dan kapasitansi per satuan panjang C' saling berhubungan dalam beberapa kasus jalur transmisi yang terdiri dari dua konduktor sempurna yang saling sejajar,

Disini ε dan µ mewakili konstanta dielektik dan konstanta permeabilitas magnetik milik konduktor yang digunakan. Dalam hal ini tidak ada arus listrik dan medan magnet di dalam konduktor (efek kulit murni, frekuensi tinggi). Arus mengalir dari satu jalur menuju jalur yang lain. Kecepatan propagasi sinyal sejalan dengan kecepatan propagasi gelombang elektromagnetik.

Lihat pula

Arus bolak-balik
Induksi elektromagnetik
Induktor
Transformator

Sumber: Wikipedia

osilator pierce 2

Oscilator pierce

Osilator atau biasa ditulis oscilator . Oscilator yang menggunakan kristal sebagai rangkaian tangki (tank circuit). Pada osilator pierce rangkaian tangki (tank circuit) menggunakan kristal yang dipasang sebagai rangkaian resonansi paralel bersama kapasitor. Oscilator pierce merupakan modifikasi dari osilator Colpitts, dimana induktor diganti dengan sebuah kristal sebagai rangkaian tangki (tank circuit). Rangkaian oscilator pierce dibangun menggunakan rangkaian penguat transistor 1 tingkat dengan konfigurasi common-emitor. Berikut adalah gambar rangkaian oscilator pierce menggunakan kristal.

Rangkaian Oscilator Pierce Dengan Kristal

Pada rangkaian oscilator pierce diatas tegangan bias basis transistor diberikan melalui R1 dan R2 kemudian bias kolektor diberikan melalui R3. Rangkaian tangki (tank circuit) oscilator pierce di bangun oleh Y1, C1 dan C2 kemudian jaringan umpan balik oscilator menggunakan kapasitor C3.

Pada saat sumber tegangan DC diberikan ke rangkaian oscilator pierce diatas, arus bias basis mengalir melalui R1 dan bias kolektor melalui R3. Pada saat yang sama C3 melalukan pengisian hingga penuh dan begitu juga dengan C1. Kemudian transistor konduk dan C3 melakukan pengosongan muatan dan terjadi perubahan polaritas pada C2 dan kristal mendapat sinyal umpan balik sehingga rangkaian tangki (tank circuit) bekerja dengan frekuensi resonansi sesuai frekuensi resonansi kristal 3,58MHz.

Pengoperasian osilator Pierce didasarkan pada jaringan umpan balik yang dipasang dari kolektor ke basis melalui C1 dan C2. Kemudian transistor memberikan kombinasi pergeseran fase sebesar 180°. Keluaran dari rangkiaan transistor common-emitor mengalami pembalikan bertujuan agar sefase atau sebagai umpan balik regeneratif. Nilai C1 dan C2 menentukan besarnya tegangan umpan balik. Sekitar 10 – 50 % dari keluaran dikirim kembali sebagai umpan balik untuk memberikan energi kembali ke kristal. Jika kristal mendapatkan energi yang tepat, frekuensi resonansi yang dihasilkan akan sangat tajam. Kristal akan bergetar pada selang frekuensi yang sangat sempit. Sinyal output rangkaian oscilator pierce ini memiliki frekuensi sangat stabil dan tidak melebar.

Balast elektronik

"Pengimbang elektronik"  atau biasa disebut ballast adalah sebuah peranti yang berfungsi membatasi arus pada sirkuit elektronik. Berbagai jenis ballast dapat ditemui. Bisa sesederhana resistor deret seperti pada LED dan lampu neon kecil. Untuk daya yang lebih tinggi, terlalu banyak daya yang dibuang pada ballast resistif, jadi peranti alternatif digunakan berdasarkan reaktansi dari induktor, kondensator atau keduanya. Akhirnya, ballast bisa menjadi sangat rumit seperti ballast elektronik terkontrol  pada lampu pendar.

Kebutuhan akan pembatasan arus

Ballast digunakan ketika beban elektrik tidak dapat membatasi penggunaan arus sendiri dengan baik. Biasanya terjadi pada peranti yang menunjukkan karakteristik resistansi negatif pada pencatu daya. Jika peranti seperti ini disambungkan pada pencatu daya tegangan konstan, ini akan mengambil arus yang akan terus bertambah hingga peranti ini hancur atau menyebabkan pencatu daya mengalami kegagalan. Untuk mencegah hal ini, sebuah ballast memberikan karakteristik resistansi positif atau reaktansi untuk membatasi arus pada harga yang dibutuhkan. Dengan kata lain, ballast memberikan peranti resistansi negatif sebuah kondisi kerja yang benar dengan mengubahnya menjadi peranti resistansi stabil. Contoh dari peranti resistansi negatif adalah lampu lucutan gas. Pengimbang juga bisa digunakan untuk dengan sengaja mengurangi arus pada peranti yang sudah beresistansi stabil. Walaupun LED adalah peranti resistansi positif, LED tidak mempunyap resistansi yang cukup untuk pengatur penggunaan arusnya ketika disambungkan ke pencatu daya terkontrol tegangan, jadi ballast digunakan untuk mengontrol arus yang mengaliri LED. Karena daya LED yang sangat kecil, biasanya digunakan pengimbang resistor sederhana.

Resistor

Maksud dari resistor pengimbang/ballast terutama merujuk pada resistor yang mengkompensasi perubahan normal ataupun insidental pada keadaan fisik sistem. Ini bisa merupakan resistor tetap ataupun resistor variabel.

Resistor tetap

Sebagai contoh sederhana, beban daya rendah seperti lampu neon dan LED biasanya menggunakan resistor tetap. Karena resistansi resistor pengimbang relatif besar daripada resistansi beban, resistor mengendalikan arus pada sirkuit, bahkan saat mengimbangi resistansi negatif pada lampu neon. Istilah ini bisa juga diartikan sebuah komponen pada mesin otomotif yang mengurangi tegangan catu ke sistem pengapian setelah mesin berhasil dihidupkan. Karena menghidupkan mesin menyebabkan beban berat pada baterai, tegangan pada sistem dapat jatuh saat penghidupan mesin. Untuk membuat mesin hidup, sistem pengapian harus didesain untuk beroperasi pada tegangan rendah. Tetapi setelah proses penghidupan mesin selesai, tegangan operasi kembali normal, tegangan ini akan membeban-lebih sistem pengapian yang didesain untuk tegangan rendah. Untuk menhindari masalah ini, resistor pengimbang disisipkan dalam deret pada tegangan catu sistem pengapian. Sistem pengapian elektronik modern tidak membutuhkan resistor pengimbang karena sudah cukup fleksibel untuk beroperasi pada tegangan rendah maupun tegangan operasional. Pada beberapa penerima AC/DC lawas, pemanas tabung hampa disambungkan dalam deret. Sejak penurunan tegangan pada seluruh filamen seringkali lebih rendah daripada tegangan catu, kadang-kadang kelebihan tegangan harus dibuang. Sebuah resistor pengimbang sering digunakan untuk penggunaan ini karena murah dan bekerja baik pada AC maupun DC. 

Resistor variabel sendiri 

Beberapa resistor pengimbang memiliki karakteristik peningkatan resistansi sesuai dengan kenaikan arus yang melewatinya, dan pengurangan resistansi saat arus berkurang. Secara fisik, beberapa peranti dibuat seperti lampu pijar. Seperti filamen wolfram pada lampu pijar biasa, jika arus listrik meningkat, resistor pengimbang memanas, menambah resistansinya, sehingga kejatuhan tegangan meningkat. Jika arus menurun, resistor pengimbang mendingin, resistansinya jatuh, dan kejatuhan tegangan berkurang. Jadi resistor pengimbang mengurangi variasi pada tegangan. Karakteristik ini dapat menuju pada kontrol arus yang lebih presisi daripada resistor tetap. Borosan daya pada pengimbang juga dikurangi. Pengimbang sendiri pada lampu uap raksa menggunakan lampu pijar biasa, dan cahaya dari lampu pijar dimanfaatkan untuk memberikan spektrum cahaya merah yang kurang diproduksi oleh lampu uap raksa.

Baca pula

Pengimbang elektronik Pengimbang lampu pendar
Langsung hidup
Cepat hidup
Hidup terprogram
pengosongan intensitas tinggi (HID)
Lampu pendar (TL) Lampu uap raksa (merkuri)
Lampu neon
Lampu natrium (sodium)

Sumber: Wikipedia

Teori Dasar Osilator

(Blok Diagram Osilator)

Osilator adalah suatu alat yang merupakan gabungan elemen - elemen aktif dan pasif untuk menghasilkan bentuk gelombang sinusoidal atau bentuk gelombang periodik lainnya.
Vgh
Suatu osilator memberikan tegangan keluaran dari suatu bentuk gelombang yang diketahui tanpa penggunaan sinyal masuk dari luar.

Osilator mengubah daya arus searah (dc) dari catu daya ke daya arus bolak - balik (ac) dalam beban. Dengan demikian fungsi osilator berlawanan dengan penyearah yang mengubah daya searah ke daya bolak - balik.

Suatu osilator dapat membangkitkan bentuk gelombang pada suatu frekuensi dalam batas beberapa siklus tiap jam sampai beberapa ratus juta siklus tiap detik. Osilator dapat hamper secara murni menghasikan gelombang sinusoidal dengan frekuensi tetap, ataupun gelombang yang hanya dengan harmonic.

Osilator umumnya digunakan dalam pemancar dan penerima radio dan televisi, dalam radar dan dalam berbagai sistem komunikasi.

Jenis - Jenis Osilator

Osilator dapat diklasifikasikan dalam berbagai cara. Tergantung kepada alam bentuk gelombang yang dibangkitkan, osilator dapat dibagi menjadi dua kategori:
¤ Osilator sinusoidal atau osilator harmonic dan,
¤ Osilator relaksasi.

Osilator sinusoidal menghasilkan bentuk gelombang sinusoidal atau mendekati sinusoidal pada frekuensi tertentu.

Osilator relaksasi menghasilkan bentuk gelombang bukan sinusoidal seperti gelombang segiempat dan gelombang gigi gergaji.

Osilator dapat pula digolongkan pada alat - alat tertentu yang menghasilkan osilasi. Pada penggolongan ini, osilator dapat merupakan jenis resistansi negatif atau jenis umpan balik.

Osilator resistansi negatif menggunakan alat aktif yang memproses lengkung karakteristik arus tegangan dengan kemiringan negatif dalam daerah operasinya. Dioda kanal merupakan alat resistansi negatif yang digunakan dalam resistor.

Osilator umpan - balik sebaliknya, mempunyai penguat umpan - balik regeneratif (positif), dimana perolehan lingkar juga diatur sedemikian sehingga perolehan keseluruhan menjadi tidak terhingga.

Baik osilator sinusoidal maupun osilator relaksaasi dapat merupakan jenis resistansi negatif dan jenis umpan-balik.

Osilator sinusoidal jenis umpan - balik dapat digolongkan lebih lanjut menjadi osilator LC (indktor - kapasitor) dan RC (tahanan kapasitor).

Osilator sinusoidal kadang - kadang digolongkan menurut frekuensi sinyal yang dihasilkan. Jadi osilator yang membangkitkan sinyal dalam daerah frekuensi audio dikenal sebagai osilator frekuensi audio.

Demikian pula, osilator yang menghasilkan sinyal - sinyal daerah frekuensi radio dinamakan osilator frekuensi radio, dan seterusnya.

Klasifikasi osilator didasarkan pada daerah frekuensi yang dihasilkan. Osilator Frekuensi Audio (AF) beberapa Hz - 20 KHz Osilator Frekuensi Radio (RF) 20 KHz - 30 MHz Osilator Frekuensi Sangat Tinggi (VHF) 30 MHz - 300 MHz Osilator Frekuensi Ultra Tinggi (UHF) 300 MHz - 3 GHz Osilator Gelombang Mikro 3 GHz - Beberapa GHz.

Osilator Pierce

Osilator Pierce sederhana

Osilator Pierce adalah salah satu jenis osilator elektronik yang ditemukan oleh George W. Pierce (1872-1956). Osilator Pierce merupakan turunan dari osilator Colpitts. Secara umum, sumber pewaktu (clock/timer) pada rangkaian elektronik digital adalah berjenis Pierce, karena rangkaian ini dapat dibuat dengan menggunakan komponen yang sedikit, misal inverter, resistor, kapasitor, dan kristal kuarsa. Biaya pembuatannya tergolong murah dan frekuensi yang dihasilkan cukup stabil.

Frekuensi resonansi

Rangkaian ekivalen osilator kristal secara umum menunjukkan ada dua kemungkinan keadaan resonansi, yaitu:

Resonansi deret



Resonansi jajar



Namun karena ,  kedua frekuensi saling berdekatan sekali.

Lihat pula
Osilator (elektronik)
Osilator Clapp
Osilator Colpitt
Osilator Pierce 2
Osilator sumbatan

Sumber: Wikipedia

Osilator sumbatan

Osilator sumbatan adalah salah satu osilator yang paling efektif untuk memproduksi pulsa-pulsa umur pendek dengan tepi-tepi cepat dan siklus aktif rendah. Salah satu penerapannya adalah sebagai generator pulsa clock dalam sistem digital. Transistor daya rendah dapat dipakai untuk membangkitkan pulsa-pulsa berdaya relatif tinggi karena siklus aktifnya rendah. Daya yang diboroskan rata-rata adalah kecil karena transistor hanya hidup sebentar selama periode siklus. Umpanbalik positif osilator adalah melalui transformator pulsa kecil di antara kalang kolektor dan kalang basis.

Cara Kerja

Bila untuk pertamakalinya daya dihidupkan, Transistor akan mati sampai tegangan yang membentangi kondensator naik sedikit diatas 0.6 V. Transistor mulai menghantar dan arus kolektor mengalir melalui lilitan primer transformator. Karena ada umpanbalik positif, arus kolektor yang berubah menginduksikan gaya elektromotif dalam lilitan sekunder yang memaksa transistor menghantar lebih lanjut. Dengan cepat sekali transistor hidup dan jenuh, tegangan kolektornya jatuh sampai sekitar 0.1 V (VCE(sat)). Setelah berlangsung sebentar, arus kolektor berhenti berubah, disebabkan oleh penguatan transistor atau kejenuhan transformator. Bila hal ini terjadi, medan magnet dalam transformator runtuh dan gaya elektromotif basis jatuh. Transistor mulai mati dengan tegangan kolektornya naik menuju +VCC. Umpanbalik dengan cepat mematikan transistor dan gelombang basis menuju negatif, tegangan puncak yang membentangi kondensator kira-kira nVCC dengan n adalah perbandingan lilitan transformator. Transistor masih tetap mati sementara kondensator mengisi muatan secara eksponensial melalui resistor. Segera setelah tegangan kondensator mencapai +0.6 V, transistor menghantar lagi dan siklus diulang. Sebuah diode dipasang membentangi primer transformator untuk menindas gaya elektromotif lawan yang ditimbulkan ketika transistor mulai mati.

Lihat pula
Gallery
Osilator
Osilator Clapp
Osilator kristal
Osilator Collpit

Sumber: Wikipedia